笔记参考：emofunc-牛客博弈论课程课件

博弈的基本概念

组合游戏

1. 两个玩家
2. 一个状态集合
3. 游戏规则是指明玩家在一个状态下可以移动到哪些其它状态
4. 玩家轮流进行移动
5. 如果当前处于某个状态，玩家根据规则无法移动，则游戏结束
6. (大部分时候)无论玩家如何选择，游戏会在有限步以内结束

组合游戏是非常常见的博弈模型

经典模型

• Bash 游戏：一堆石子，轮流取，每次最少取 $1$ 个，最多取 $m$ 个，无法取者输
• Nim 游戏：假设有 $n$ 堆石子，第 $i$ 堆石子一开始有 $x_i$ 个，Alice 和 Bob 轮流取石子，每次当前玩家可以从某堆石子中取出一个到多个石子（可以取完，但不能不取），无法取石子的玩家输。

Nim 游戏是非常常见的博弈模型，很多问题可以化归到 Nim 游戏

基本概念

• P 态: 走到这个状态的玩家 (previous player) 赢的状态
• N 态: 从这个状态走的玩家 (next player) 赢的状态
• 正常规则 (normal play rule): 终态是 P 态（无法走的人输）
• 反常规则 (mis`ere play rule): 终态是 N 态（无法走的人赢）
• 平等游戏 (impartial game): 规则对两个玩家是一致的
• 不平等游戏 (partizan game): 规则对两个玩家不一致

SG 函数

基本概念

• 图游戏：给定一个有向图 $G=(V,E)$ ,其中 $V$ 是非空的结点集，$E$ 是有向边集。两个人在图 $G$ 上进行游戏。从起始结点 $x_0$ 出发，轮流移动。每一轮当前玩家可以从当前结点 $x$ 按照有向边集移动到下一个结点，把 $x$ 可以一步移动到的结点集合记为 $F(x)$。如果 $F(x)$ 为空，则 $x$ 为终止结点，此时玩家不能移动，游戏结束。(在正常游戏下不能移动的玩家输)

图游戏是一种组合游戏的抽象描述

• SG 函数：
• 定义有向无环图 $G=(V,E)$ 的 SG 函数是一个结点集 $V$ 到非负整数 $\mathbb{Z}\geq0$ 的映射
  $g:V\to\mathbb{Z}{\geq0}$，满足 $g(x)=\operatorname{mex} \left{g(y)\mid y\in F(x)\right}$
  • SG 函数 vs PN 态 (正常游戏下）
  • $x$ 是 P 态当且仅当 $g(x) = 0$
  • $x$ 是 N 态当且仅当 $g(x) > 0$
• 组合游戏的和：给定多个组合游戏，可以用如下方式把它们进行组合。每个游戏都有一个初始状态，每次当前玩家可以选择一个游戏，并按照该游戏的规则移动一次，如果轮到当前玩家时，所有游戏都不能移动，则该玩家输(正常规则)。称这个新的组合游戏为这些组合游戏的和。

Nim 游戏就是一个组合游戏的和

SG 定理

• 定理内容：假设有 $n$ 个组合游戏 $G_1,G_2,…,G_n$, 记 $g_i$ 为第 $i\left(1\leq i\leq n\right)$ 个组合游戏的 SG 函数，则它们的和 $G=G_1+G_2+…+G_n$ 的 SG 函数
  $g(x)=g((x_1,x_2,…,x_n))=g_1(x_1)\oplus g_2(x_2)\oplus…\oplus g_n(x_n)$
• 定理推论：假设 $G=G_1+G_2+…+G_n$
  • $x=(x_1,x_2,…,x_n)$ 是 P 态当且仅当 $g_1(x_1)\oplus g_2(x_2)\oplus…\oplus g_n(x_n)=0$
  • $x=(x_1,x_2,…,x_n)$ 是 N 态当且仅当 $g_1(x_1)\oplus g_2(x_2)\oplus…\oplus g_n(x_n)>0$

树上的 Green Hackenbush

• Green Hackenbush：有一个无向图，其中一些结点在地面 (ground) 上，轮流操作，每次操作可以任选一条边删除，如果产生了一个不与地面连接的连通分量，则这个连通分量也一并删除。不能操作的人输。
  • 树上的 Green Hackenbush：无向图是一棵树，树的根在地面上
  • Hackenbush：边分为 绿/红/蓝 三种边，玩家 1 可以删绿边和红边，玩家 2 可以删绿边和蓝边

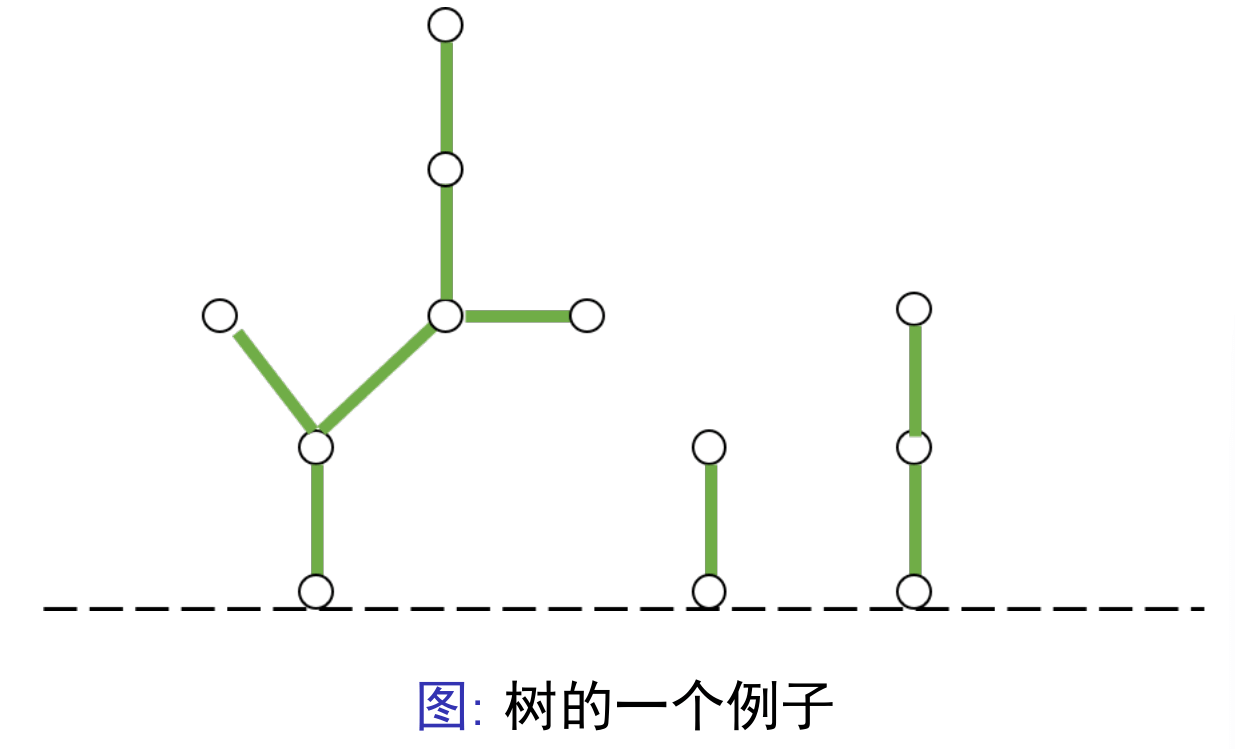
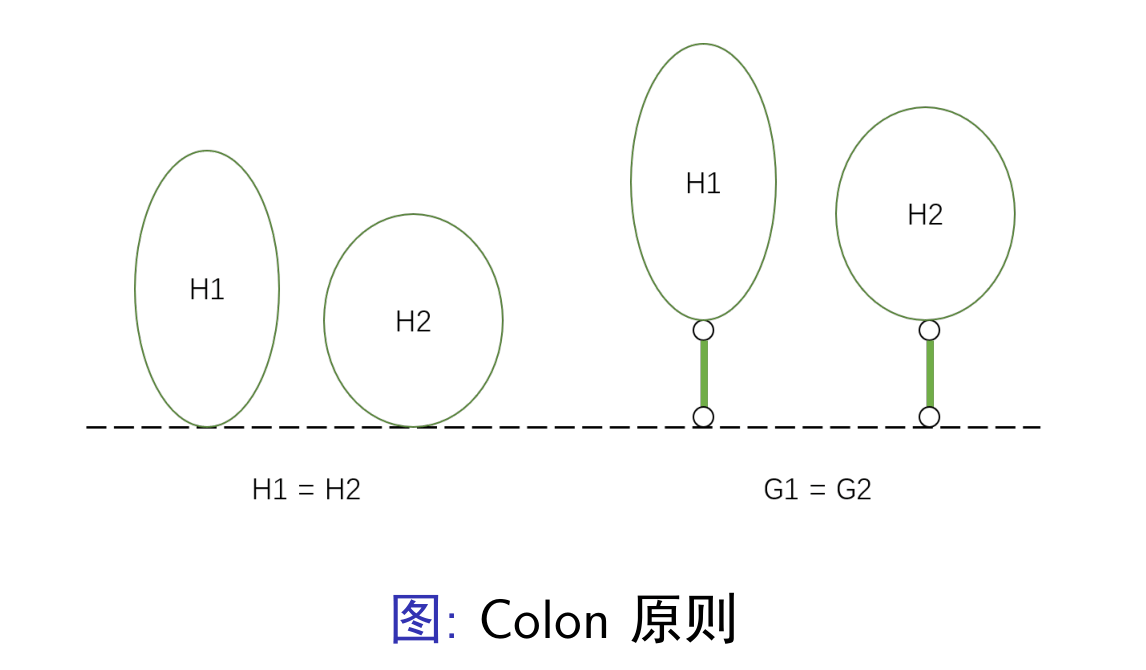
• Colon 原则（简化版）：假设 $H_1,H_2$ 是两个 Green Hackenbush 游戏，$G_1$ 是 $H_1$ 建立一个新的地面，将原地面作为一个结点，且这个结点与新的地面接触得到的游戏，$G_2$ 是 $H_2$ 以同样的方式得到的游戏。若 $g(H_1)=g(H_2)$ ,则 $g(G_1)=g(G_2)$。

经典的组合游戏

Fibonacci Nim & Zeckendorf’s Theorem

• 游戏规则：初始时有 $n$ 个石子，两个人轮流取石子。规则为
  • 先手第一次可以取 $1$ 到 $n-1$ 个石子
  • 之后每一次，可取的数量为 $1$ 到上一个人取的石子数的 $2$ 倍
    不能取的人输
• Zeckendorf’s Theorem：每个正整数可以唯一的写成一些不相邻的 Fibonacci 数的和 (其中 Fibonacci 数${F_n}$满足 $F_1=1,F_2=2$ 且 $F_n=F_{n-1}+F_{n-2}(n>2)$）
• PN 态：局面是 P 态当且仅当 $n$ 为 Fibonacci 数
• 必胜策略：
  • 若 $n$ 不是 Fibonacci 数，假设 $n = F_{x1} + F_{x2} + \dots + F_{xk}$，其中 $x_i > x_{i+1} + 1 (1 \le i <k)$，则先手可取 $F_{xk}$。
  • 若 $n = Fx$ 是 Fibonacci 数，后手只需要取 $n-m$ 斐波那契分解后的 $F_{xk}$ 即可（可以证明一定可取）。

Chomp 游戏

• 游戏规则：一开始有 $n\times m$ 块饼干，排列成一个 $n$ 行 $m$ 列的矩形，其中位于 $(1,1)$ (左上角) 的饼干是有毒的。两个人轮流进行游戏，每次可以取当前还没被取的一块饼干 $(x,y)$, 并把所有 $(i,j)$ 满足 $i\geq x$ 或 $j\geq y$ 的饼干都吃掉。吃到有毒的饼干就会死。请问先手死还是后手死。
• PN 态：所有 $n,m$, 满足 $\max(n,m)>1$ 的矩形均为 N 态
  • 证明：如果先手取 $(n,m)$ 时后手存在必胜策略 $(a,b)$, 则先手可以直接取 $(a,b)$。
• 必胜策略：没有一般的必胜策略。
• 有限偏序集上的 Chomp 游戏：设偏序集 $(S,\leq)$, 其中 $S$ 有限，且 $S$ 中存在最小元。一开始 $T=S$, 可以取 $x\in T$, 并把 $x<y$ 的元素 $y$ 从 $T$ 中去掉。取到最小元的人输。
  • 结论：如果偏序集 $(S,\leq)$ 存在最大元，且 $|S|>1$, 则先手必胜

Wythoff 游戏 & Beatty 序列

• 游戏规则：有两堆石子，石子数分别为 $n,m$。两个玩家轮流进行，轮到一方的时候，该玩家可以做
  • 从其中一堆石子中取走 $x\geq1$ 个 ($x$ 不能超过该堆的石子数);或
  • 从两堆石子中同时取走 $x\geq1$ 个 ($x$ 不能超过任意一堆的石子数)。
  • 如果轮到某方的时候，玩家无法操作，则该玩家输
• PN 态：所有满足以下关系的 $(a_i,b_i),a_i \le b_i$ 为 P 态（其中 $a_i,b_i$ 为两堆石子的石子数）：
  • 序列 $(a_i),(b_i),i \ge 0$, 满足 $a_i=\lfloor\phi i\rfloor$，$b_i=\lfloor\phi^2i\rfloor$，其中 $\phi=\frac{1+\sqrt{5}}2$ 是黄金分割比。
• Beatty 序列：一个正无理数 $r$ 生成的 Beatty 序列是指这样的一个序列 $B_r=(\lfloor ri\rfloor)_{i\geq 1}$
  • Rayleigh 定理：假设正无理数 $r>1,s$ 满足 $\frac1r+\frac1s=1$, 则 $B_r$ 与 $B_s$ 是全体正整数的一个分割。即任意一个正整数存在且仅存在于 $B_r$ 和 $B_\mathrm{s}$ 的其中一个序列。
• Wythoff 游戏的 k扩展（游戏规则第二条改成“从两堆石子中分别取走 $x,y\geq1$ 个,满足 $|x-y|\leq k$”）：通过联立 $\frac{1}{r}+\frac{1}{s}=1$ 和 $\lfloor si \rfloor – \lfloor ri \rfloor= i(k+1)$ 即 $s = r+k+1$ 两个方程来解出 $r,s$ 作为 Beatty 序列。

二分图博弈

• 游戏规则：给出一个二分图和一个起始点 $H$，两人轮流操作，每次只能选择一个与当前点相邻的之前没有被走过的点，并走到该相邻点，不能走的人输。
• PN 态：如果二分图的最大匹配一定包含起始点 $H$，则先手必胜，否则先手必败。
• 必胜策略：
  • 如果 $H$ 一定在最大匹配上，先手按 $H$ 的匹配边走到下一个点。
  • 如果 $H$ 不在其中一个最大匹配 $\mathcal{M}$ 上，不管先手走哪个点 $P$, 后手按 $P$ 的匹配边走到下一个点。